Answer:
Option (3) is correct.
The zero of given function
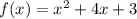 is x= -1 and x= -3.
is x= -1 and x= -3.
Explanation:
Consider the given function
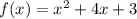
We need to find the zero of the above function. Put f(x)=0
then ,
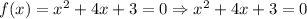
The above function represents a quadratic equation
We can solve the quadratic equation by splitting middle term method,
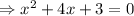
We can write 4x as x+ 3x ,
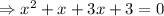
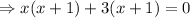
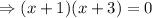
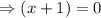 or
or
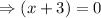
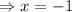 or
or
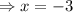
Thus, the zero of given function
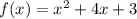 is x= -1 and x= -3.
is x= -1 and x= -3.