Answer:
Cone: h =
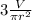
Cylinder: h =
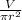
Explanation:
- the formula you described is not the formula for the volume of a cone as it is V =
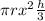
- to find the height you simply rearrange the formula, so the formula to calculate the height of the cone is:
- h =
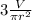
- based on the formula you described, it is closer to a cylinder and the formula for the volume of a cylinder is: V =
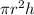
- once again, to find the height you simply rearrange the formula, so the formula to calculate the height of the cone is:
- h =
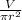
hope this helps :)