Question

An executive invests $28000, some at 8% and the rest at 6% annual interest. If he receive annual return of $2000 how much is invested at each rate?

Answer 1

$16,000 at 8% annual interest.

$12,000 at 6% annual interest.

Explanation:

Let x be amount invested at a rate of 8% annual interest and y be the amount invested at a rate of 6% annual interest.

We have been given that an executive invests $28000, some at 8% and the rest at 6% annual interest. We can represent this information as:

`x+y=28,000...(1)`

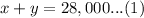
We are also given that he received annual return of $2000. We can represent this information as:

`((8)/(100))x+((6)/(100))y=2,000...(2)`

`0.08x+0.06y=2,000...(2)`

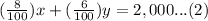
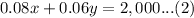
We will use substitution method to solve our system of equations. From equation (1) we will get,

`x=28,000-y`

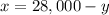
Substituting this value in equation (2) we will get,

`0.08(28,000-y)+0.06y=2,000`

`2240-0.08y+0.06y=2,000`

`2240-2240-0.08y+0.06y=2,000-2240`

`-0.08y+0.06y=2,000-2240`

`-0.02y=-240`

`(-0.02y)/(-0.02)=(-240)/(-0.02)`

`y=12,000`

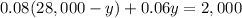
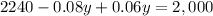
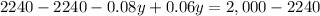
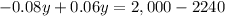
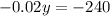
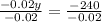
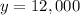
Therefore, the executive has invested $12,000 at a rate of 6% annual interest.

Upon substituting y=12,000 in equation (1) we will get,

`x+12,000=28,000`

`x+12,000-12,000=28,000-12,000`

`x=16,000`

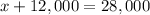
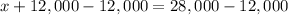
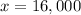
Therefore, the executive has invested $16,000 at a rate of 8% annual interest.

Answer 2

Amount invested at 8% interest rate = $16000

Amount invested at 6% interest rate = $12000

Explanation:

Total amount invested = $28000

Let amount invested with 8% interest rate be $x

Then amount invested at 6% interest rate = 28000 - x

Now, Total return = Return from 8% interest rate + Return from 6% interest rate

⇒ 2000 = 8% (in decimal form) × amount invested + 6%(in decimal form) × Amount invested

⇒ 2000 = 0.08 × x + 0.06 × (28000 - x)

⇒ 2000 = 0.02·x + 1680

⇒ x = 16000

Hence, Amount invested at 8% interest rate = $16000

And, Amount invested at 6% interest rate = 28000 - 16000

= $12000