Answer:
We are given:
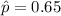
Margin of error
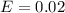
Confidence level = 0.99
We need to find the sample size to estimate the proportion of people who carry the TAS2R388 gene.
The formula for finding the sample size is:
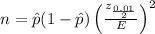
Where:
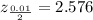 is the critical value at 0.01 significance level.
is the critical value at 0.01 significance level.
Therefore, the required sample size is:
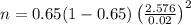
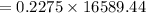
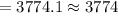
Therefore, the required sample size is 3774