Answer:
Option C is correct.
Constant of variation k = -0.5
Explanation:
The direct variation says that:
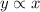
then, the equation is of the form:
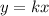 .....[1] where k is the constant of variation.
.....[1] where k is the constant of variation.
Given the table:
x f(x)=y
0 0
2 -1
4 -2
7 -3.5
Consider any values from the tables
x = 4 and y=f(x) = -2
Substitute these values in equation [1] we have;
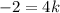
Divide both sides by 4 we get;
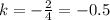
Therefore, the constant of variation is, -0.5