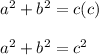By the Angle-Angle Similarity Postulate, △YXZ ~ △YZQ and △YXZ ~ △ZXQ. Since similar triangles have proportional sides, a/c = f/a and b/c = e/b. Solving the equation for
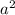 and
and
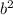 gives
gives
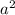 = cf and b^2 =ce. Adding these together gives
= cf and b^2 =ce. Adding these together gives
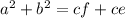 . Factoring out the common segment gives
. Factoring out the common segment gives
 . Using the segment addition postulate gives
. Using the segment addition postulate gives
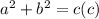 , which simplifies to
, which simplifies to
 .
.
In Mathematics and Euclidean Geometry, AAS is an abbreviation for Angle-Angle-Side and it states that when two (2) angles and the non-included side (adjacent to only one of the angles) in two triangles are all equal, then the triangles are said to be congruent.
Based on the Angle-Angle Similarity Postulate, triangle YXZ is similar to triangle YZQ and triangle YXZ is similar to triangle △ZXQ. Since all similar triangles have proportional sides, we have;
a/c = f/a and b/c = e/b.
By solving the equation for
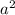 and
and
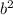 , we have;
, we have;
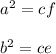
By adding the above together, we have;
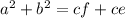 .
.
By factoring out the common segment, we have;
 .
.
By using the segment addition postulate, we have;