Explanation:
Since we have given that
Given : In triangle ABC, P is the mid point of AB, and Q is the midpoint of AC.
To prove : BC=2PQ
Construction : Join PQ such that PQ║BC.
Proof: Since P and Q are the midpoints of AB and AC respectively.
Using Mid point theorem, it states that the line segments joining the midpoints is parallel to the third side and equal to half of the third side.
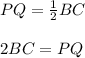
Hence proved.