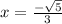Answer:
1.
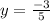
2.
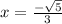
Explanation:
Ques 1: We are given that the point
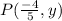 lies on a unit circle and is in the 3rd quadrant.
lies on a unit circle and is in the 3rd quadrant.
The equation of the unit circle is
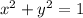 .
.
Substituting the values, we get,
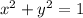
⇒
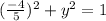
⇒
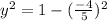
⇒
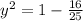
⇒
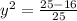
⇒
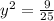
⇒
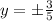
Since, the point P lies in the 3rd quadrant i.e. the value of y will be negative.
So,
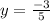 .
.
Ques 2: We are given that the point
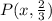 lies on a unit circle and is in the 2nd quadrant.
lies on a unit circle and is in the 2nd quadrant.
The equation of the unit circle is
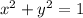 .
.
Substituting the values, we get,
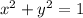
⇒
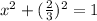
⇒
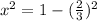
⇒
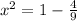
⇒
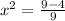
⇒
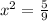
⇒
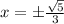
Since, the point P lies in the 2nd quadrant i.e. the value of x will be negative.
So,