For this case we must find the volume of the figure composed of a parallelepiped and a pyramid. The volume of the parallelepiped is given by:
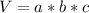
Where a, b and c are the sides
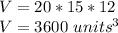
For its part, the volume of the pyramid is given by:
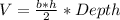
Where:
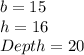
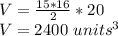
Thus, the total volume is given by the sum of the volumes.
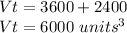
Answer:
D