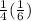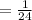Answer:
Probability of choosing a heart and rolling a 2 =
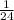
Explanation:
Let A be the event of choosing a heart from a standard deck of cards and
B be the event of rolling a 2.
Clearly, A and B are independent events as none of the events does not affect the probability of occurrence of other event.
Therefore, P(A∩B) = P(A) × P(B)
P(A) =
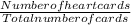

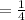
P(B) =

P(A∩B) = P(A) × P(B)
=