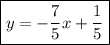A)
The slope-intercept form:

m - slope
b - y-intercept
The formula of a slope:
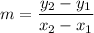
We have the points (2, 5.1) and (-1, -0.5). Substitute:
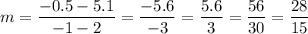
Therefore we have:
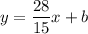
Put the coordinates of the point (-1, -0.5) ot the equation:
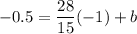
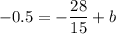 multiply both sides by 2
multiply both sides by 2
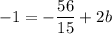 add
add
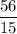 to both sides
to both sides
 divide both sides by 2
divide both sides by 2
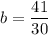
Answer:
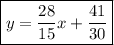
-------------------------------------------------------------------------
B)
We have the points (-2, 3) and (3, -4).
Calculate the slope:

Therefore we have:

Put the coordinates of the point (-2, 3) to the equation of a line:
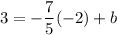
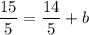 subtract
subtract
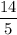 from both sides
from both sides
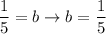
Answer: