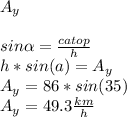Question

A helicopter is traveling at 86.0 km/h at an angle of 35° to the ground. What is the value of Ax? Round your answer to the nearest tenth. km/h What is the value of Ay? Round your answer to the nearest tenth. km/h

Answer 1

First thing plot a right angle with angle of elevation of 35degrees as shown in figure then use SOHCAHTOA.

Ay/Helicopter = sin 35

Ay = 86 sin 35 = 36.8237

Ax/Helicopter = cos 35

Ax = 86 cos 35 = 77.7175

Note: I ignore the negative signs coz they signify direction

Answer 2

`A_(x) =70.4 (k)/(h)`

`A_(y) =49.3(km)/(h)`

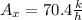
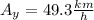
Step-by-step explanation:

Hello

the helicopter is traveling at an angle of 35° to the ground, let this angle called a (α)

if A is the magnitude of the vector that forms an angle of 35, we have a rectangle triangle, where

h=86

α=35°

by definition

`cos\alpha =(c.ady)/(h) \\h*cos\alpha =A_(x)\\ \\A_(x)=86*cos (35)\\A_(x) =70.4 (k)/(h)`

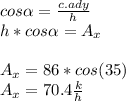
now

`A_(y)\\\\ sin\alpha =(catop)/(h) \\h*sin(a)=A_(y)\\A_(y) =86*sin(35)\\A_(y) =49.3(km)/(h)`