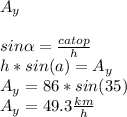Answer:
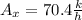
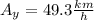
Step-by-step explanation:
Hello
the helicopter is traveling at an angle of 35° to the ground, let this angle called a (α)
if A is the magnitude of the vector that forms an angle of 35, we have a rectangle triangle, where
h=86
α=35°
by definition

now