Question

Find the sum of all positive 3-digit numbers divisible by 12.

Answer 1

First 3-digit number divisible by 12 is 108.

Last 3-digit number divisible by 12 is 996.

108 = 12 · 9

996 = 12 · 83

From 108 to 996 are 83 - 9 + 1 = 75 numbers divisible by 12.

108 is the first term of the arithmetic sequence.

996 is the 75th term of the arithmetic sequence.

Use the formula of a sum of terms of an arithmetic sequence:

`S_n=(a_1+a_n)/(2)\cdot n`

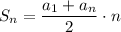
We have:

`a_1=108,\ a_(75)=996,\ n=75`

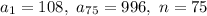
Substitute:

`S_(75)=(108+996)/(2)\cdot75=(552)(75)=41,400`

Answer: 41,400