First 3-digit number divisible by 12 is 108.
Last 3-digit number divisible by 12 is 996.
108 = 12 · 9
996 = 12 · 83
From 108 to 996 are 83 - 9 + 1 = 75 numbers divisible by 12.
108 is the first term of the arithmetic sequence.
996 is the 75th term of the arithmetic sequence.
Use the formula of a sum of terms of an arithmetic sequence:
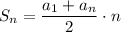
We have:
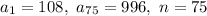
Substitute:
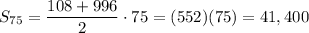
Answer: 41,400