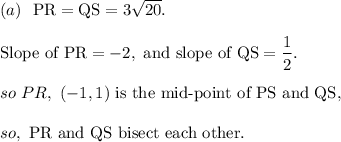Answer: The first option is correct.
Step-by-step explanation: Given that the vertices of square PQRS are P(−4, 7), Q(5, 4), R(2,−5) and S(−7,−2). So, PR and QS are its two diagonals.
First, we will measure PR and QS as follows.
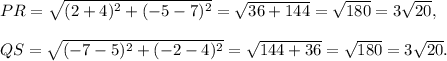
Therefore, PR = QS = 3√20.
Now, slope of PR is
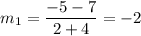
and slope of QS is
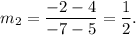
Hence, PR ⊥ QS.
Again, mid-point of PR is
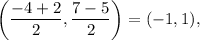
and mid-point of QS is
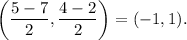
Thus, the correct option is