Question

Write the linear inequality shown in the graph. The gray area represents the shaded region.

A. y ≤ 3x + 4

B. y ≤ 3x – 4

C. y ≥ 3x + 4

D. y ≥ 3x – 4

Answer 1

ANSWER

`y \ge 3x - 4`

EXPLANATION

The given line passes through (2,2) and (0,-4)

The slope of the given line is


`m = (2 - - 4)/(2 - 0) = (6)/(2) = 3`

The line has a y-intercept of


`c = - 4`

The equation is given by

`y = mx + c`

Thus,


`y = 3x - 4`

Since the right half plane is shaded the required inequality is



`y \ge3x - 4`

Answer 2

Answer: C.
`y\geq3x-4`

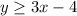
Explanation:

1. The graph indicates that the line intersect the y-axis at -4.

2. Then, you must choose any point that are located within the region and replace them to see if the inequality is satisfied. Therefore, you have:

Point (0,2):

`y\geq3x-4\\2\geq3(0)-4\\2\geq-4`

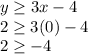
(This is true)

3. Therefore, you can conclude that the answer is the option C.