According to Dalton's law of partial pressure: The pressure exerted by a mixture of gases is sum partial pressure of each gas exert on the container.
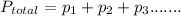
Here we have mixture of three gases so the total pressure of three gases will be sum of their individual or partial pressures
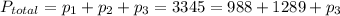
Therefore the partial pressure of third gas will be
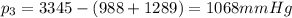
The pressure of gas#3 is 1068mmHg