ANSWER
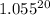
times larger.
Step-by-step explanation
The given function is
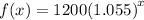
The average rate of change between years 21 and 25 is
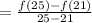
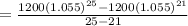

The average rate of change between years 1 and 5 is
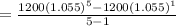
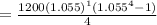
Hence the average rate of change between years 21 and 25 is
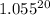
times larger than the average rate of change between years 1 and 5.