Question

3y−13≥−9 and 3y−13≤−1

Use in interval notation please

Answer 1

Explanation:

3y-13>-9

3y-13<-1

3y>4

3y<12

12>3y>4

y=2,3,4

Answer 2

`\left[ (4)/(3),4 \right]`

Explanation:

Inequality 1

`3y-13\geq -9`

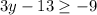
Add 13 to both sides:

`\implies 3y-13+13\geq -9+13`

`\implies 3y\geq 4`

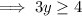
Divide both sides by 3:

`\implies (3y)/(3)\geq (4)/(3)`

`\implies y \geq (4)/(3)`

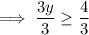
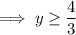
Therefore, y is equal to or bigger than 4/3.

Inequality 2

`3y-13\leq -1`

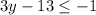
Add 13 to both sides:

`\implies 3y-13+13\leq -1+13`

`\implies 3y\leq 12`

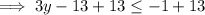
Divide both sides by 3:

`\implies (3y)/(3)\leq (12)/(3)`

`\implies y\leq 4`

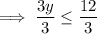
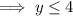
Therefore, y is equal to or smaller than 4.

Therefore, the solution to the inequalities in interval notation is:

`\left[ (4)/(3),4 \right]`