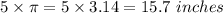Question

Celia is staring at the clock waiting for school to end so that she can go to track practice. She notices that the 5-inch-long minute hand is rotating around the clock and marking off time like degrees on a unit circle.

Part 1: How many radians does the minute hand move from 1:25 to 1:55? (Hint: Find the number of degrees per minute first.)
Part 2: How far does the tip of the minute hand travel during that time?

You must show all of your work.

Answer 1

Answer: a)
`\pi\text{ radian}`

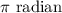
b) 15.7 inches

Explanation:

We know that the measure of complete circle is
`360^(\circ)`.

Therefore,

`60\ minutes=360^(\circ)\\\Rightarrow\ 1\ minute=(360)/(60)=60^(\circ)`

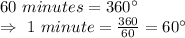
The minute hand move from 1:25 to 1:55, it means the minute have cover 30 minutes.

Now, 30 minutes=
`60*30=180^(\circ)`

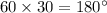
In radians, 30 minutes=
`180^(\circ)*(\pi)/(180^(\circ))`

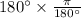
Therefore, 30 minutes=
`\pi\ radians`

Also the length of arc is given by

`l=r\theta`

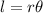
Now, for radius r= 5 inch and
`\theta=\pi`

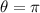
Length traveled by the tip of the minute hand travel during that time=
`5*\pi=5*3.14=15.7\ inches`