Answer:
So the Point of intersection is (-4,-2)
Which is option A
Explanation:
The given system of equations is
-0.1x - 0.8y = 2 ...................(i)
0.6x - 0.5y = -1.4 ...................(ii)
Let us take equation (i) and use method of substitution for solving it
the equation (i) is
-0.1 x - 0.8y = 2
Adding 0.8y on both sides
-0.1 x + 0.8 y - 0.8 y = 2 + 0.8 y
-0.1 x = 2 + 0.8 y
Dividing both sides -0.1
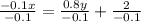
x = -8 y - 20 ..........................(iii)
Now we will use this value and put it into equation (ii) to find the value of y
Equation (ii) is
0.6 x - 0.5 y = -1.4
Put value of x
0.6(-8 y - 20) - 0.5 y =-1.4
It becomes
-4.8 y - 12 - 0.5 y = -1.4
adding 12 on both sides
-4.8 y - 0.5 y - 12 + 12 = -1.4 + 12
it becomes by solving
-5.3 y = 10.6
Dividing both sides by -5.3
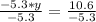
So
y = -2
Now we have the value of y putting it in equation (iii)
Equation (iii) is
x = -8 y - 20
Putting value of y
x = -8*(-2) - 20
x = 16-20
x=-4
So the Point of intersection is (-4,-2)