Answer:
It would be a straight line
Step-by-step explanation:
On a distance-time graph, an object that moves at constant speed would be represented by a straight line.
In fact, in a distance-time graph, the slope of the line corresponds to the speed of the object. We can demonstrate that. In fact:
- The speed of the object is equal to the ratio between the distance covered
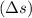 and the time taken (
and the time taken (
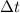 ):
):
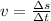
On a distance-time graph, the distance is on the y-axis while the time is on the x-axis. The slope of the line is defined as:
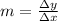
But the variation on the y-axis (
 ) is equal to the distance covered (
) is equal to the distance covered (
 ), while the variation on the x-axis
), while the variation on the x-axis
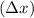 corresponds to the time taken (
corresponds to the time taken (
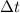 ), so the slope can also be rewritten as
), so the slope can also be rewritten as
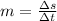
which is equal to the speed of the object. Therefore, an object moving at constant speed would be represented by a line with constant slope, which means a straight line.