Answer:
The shortest possible length for the service road is 2.88 miles.
Explanation:
According to the below diagram,
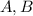 and
and
 are the positions of airport, shopping center and factory respectively.
are the positions of airport, shopping center and factory respectively.
Given that,
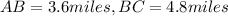 and
and
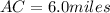
In right triangle
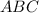

The shortest possible length for the service road from the shopping center to the highway that connects the airport and factory is
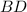 .
.
That means,
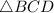 is also a right triangle in which
is also a right triangle in which
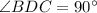 , Hypotenuse
, Hypotenuse
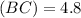 miles and
miles and
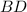 is the opposite side in respect of
is the opposite side in respect of
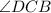 or
or
 .
.
Now in right triangle
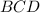
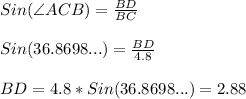
So, the shortest possible length for the service road is 2.88 miles.