Question

An engineer is designing a storage compartment in a spacecraft .The compartment must be 2 meters longer than it is wide, and its depth must be 1 meter less than its width. The volume of the compartment must be 8 cubic meters.Write an equation to model the volume of the compartment. Determine the dimensions where it produces the maximum volume. Sketch the graph

Answer 1

Answer: The dimensions are 1 m × 2 m × 4 m.

Step-by-step explanation: Given that an Engineer is designing a storage compartment in a spacecraft. The length of the spacecraft is 2 m more than its width and depth is 1 m less than its width.

We need to find the dimensions of the compartment where it produces the maximum volume.

Let, 'b' m be the width of the compartment. Then, its length will be (b + 2) and depth will be (b-1). Since the volume of the compartment is 8 cubic metres, so

`b* (b+2)* (b-1)=8\\\\\Rightarrow b(b^2+b-2)=8\\\\\Rightarrow b^3+b^2-2b-8=0\\\\\Rightarrow b^2(b-2)+3b(b-2)+4(b-2)=0\\\\\Rightarrow (b-2)(b^2+3b+4)=0.`

So, b = 2 or b² +3b + 4 = 0. Since the second quadratic equation will not give real roots and length of any thing cannot be imaginary, it must be real, so we will consider b = 2.

Hence, width = 2 m, length = 2+2 = 4 m and depth = 2-1 = 1 m.

Thus, the equation which model the volume of the compartment is

`b(b-2)(b-1)=0,`

and the dimensions are 1 m × 2 m × 4 m. Also, the sketch is attached herewith.

Answer 2

Let x be the width of the compartment,

Then according to the question,

The length of the compartment = x + 2

And the depth of the compartment = x -1

Thus, the volume of the compartment,
`V = (x+2)x(x-1) = x^3 + x^2 - 2x`

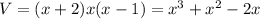
But, the volume of the compartment must be 8 cubic meters.

⇒
`x^3 + x^2 - 2x = 8`

⇒
`x^3 + x^2 - 2x - 8=0`

⇒
`(x-2)(x^2+3x+4)=0`

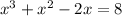
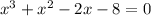
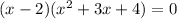
If
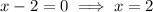`x-2=0\implies x = 2` and if
`x^2+3x+4=0\implies x = \text{complex number}`

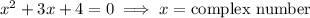
But, width can not be the complex number.

Therefore, width of the compartment = 2 meter.

Length of the compartment = 2 + 2 = 4 meter.

And, Depth of the compartment = 2 - 1 = 1 meter.

Since, the function that shows the volume of the compartment is,

`V(x) = x^3 + x^2 - 2x`

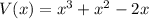
When we lot the graph of that function we found,

V(x) is maximum for infinite.

But width can not infinite,

Therefore, the maximum value of V(x) will be 8.