Answer:

Only n=9 is reasonable.
Explanation:
We have been given that the volume of the shipping box is:
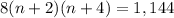 .
.
First of all we will distribute 8 to (n+2).

Using FOIL we will get,
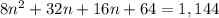

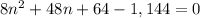
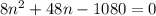
Upon dividing our equation by 8 we will get,

Now we will factor out our given equation by splitting the middle term.
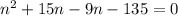
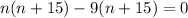
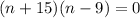
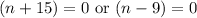

Since the volume of a box can not be negative, therefore, only one solution is reasonable, that is n=9.