Answer:
For the function,
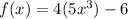 , stretches the graph by making the outputs matched to the inputs much larger than the parent function
, stretches the graph by making the outputs matched to the inputs much larger than the parent function
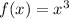 . It stretches further by being multiplied by 4 after
. It stretches further by being multiplied by 4 after
 . Lastly the graph is shifted down by 6 units.
. Lastly the graph is shifted down by 6 units.
Explanation:
When functions are transformed there are a few simple rules:
- Adding/subtracting inside the parenthesis to the input shifts the function left(+) and right(-).
- Adding/subtracting outside the parenthesis to the output shifts the function up(+) and down(-).
- Multiplying the function by a number less than 1 compresses it towards the x-axis.
- Multiplying the function by a number greater than 1 stretches it away from the x-axis.
- Multiplying by a negative or changing the leading coefficient's sign will flip the graph.
For the function,
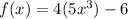 , stretches the graph by making the outputs matched to the inputs much larger than the parent function
, stretches the graph by making the outputs matched to the inputs much larger than the parent function
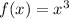 . It stretches further by being multiplied by 4 after
. It stretches further by being multiplied by 4 after
 . Lastly the graph is shifted down by 6 units.
. Lastly the graph is shifted down by 6 units.