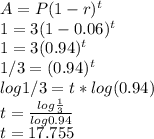Answer:
17.8 years
Explanation:
To find the population in a future year, use the formula:
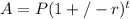
where A is the amount, p is the starting population, r is 6% or 0.06, and t is the number of years.
Since the population is decreasing it is subtraction. Here we are finding t, A=1 P =3, and r=0.06.