Answer:
The progression is Option A. convergent.
Explanation:
The given series is(
 )
)
=
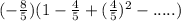
Now we can write this series as
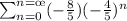
In this expression common ration is 4/5= 0.8
As we know that in geometric progression if common factor is less than one then the progression converges.
Therefore we can say that this progression is convergent.