Answer:
32/5
option D
Explanation:
Given series is 8 -2 + 1/2 - 1/8+.....
Given series is geometric
to find sum we use formula
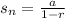
where 'a' is the first term
and r is the common ratio
to find out common ratio 'r' we divide second term by first term
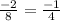
Now plug in r=-1/4 and a= 8 in the formula to find sum
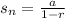
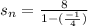
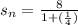
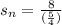
Flip the bottom fraction and multiply with 8
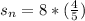
sum = 32/5