Answer:
Option C is correct.
The graph is shifted 2 units up.
Explanation:
Given the parent function:
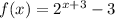
To shift the function: We will be adding the number outside the function.
i.e,
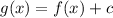
- if c > 0, then the function shifted up
- if c < 0 , then the function shifted down.
To shift the function f(x), c= 2> 1 unit up we get g(x) i.e

Therefore, the the graph f(x) change to g(x) which implies that the graph is shifted 2 units up.