Question

...... trying to find domain, range rel max rel min end behavior inc intervals dec intervals. zeros..... I'm a mom trying to help her son

Answer 1

The values are evaluated below.

Explanation:

Given function is

`-x^4-7x^3-12x^2`

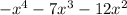
We have to find the domain, range, rel max, rel min, end behaviour, increasing or decreasing intervals and zeros of polynomial.

Domain:

The domain of a function is the set of all possible values of x for the given function.

Here domain is set of all real numbers R.

Range:

The range is the resulting y-values we get after substituting all the possible x-values.From the graph we see that

The range is
`-\infty<y<3.124`

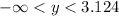
Relative maxima and minima of a function, are the largest and smallest value of the function on an entire domain of function.

Relative max of
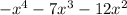`-x^4-7x^3-12x^2` is 0 at x=0

and
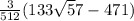`(3)/(512)(133\sqrt57-471)` at
`x=(-21)/(8)-(\sqrt57)/(8)`

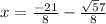
Relative min is

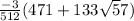`(-3)/(512)(471+133\sqrt57)` at
`x=(-21)/(8)+(\sqrt57)/(8)`

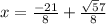
From the graph we see that

End behaviour is As
`\\x->\infty, f(x)->-\infty\\x->-\infty, f(x)->-\infty\\`

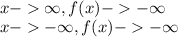
Increasing intervals and decreasing intervals are

Increasing:
`(1)/(8)(\sqrt57-21)<x<(1)/(8)(-21-\sqrt57)`

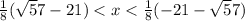
Decreasing:
`(1)/(8)(-21-\sqrt57)<x<(1)/(8)(\sqrt57-21)`

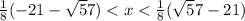
Zeroes are :

`-x^4-7x^3-12x^2=0`

⇒
`(-x^2)(x^2+7x+12)=0`

⇒
`(-x^2)(x+3)(x+4)=0`

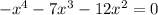
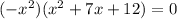
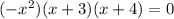
Hence, zeroes are 0, 0, -3, -4

Answer 2

Domain: (-∞,∞)

Range: (-∞,316.87].

maximum is 316.87.

zeros of f(x) are 0,0,-4,-3.

Explanation:

We are given a function f(x) as:

`f(x)=-x^4-7x^3-12x^2`

as the function is a polynomial function, hence the function is defined everywhere on the real line.

Hence, the domain of the function is all of the real line i.e. (-∞,∞).

Also the range of the function is:

since the maximum of a function is attained at 316.87 hence the range of the function is: (-∞,316.87].

Also the maximum is 316.87.

The minimum value of the function is not possible as the graph decreases at both the side of the axis.

The zeros of f(x) are the points at which f(x)=0

Hence, when f(x)=0

i.e.
`-x^4-7x^3-12x^2=0\\\\-x^2(x^2+7x+12)=0\\\\-x^2(x^2+4x+3x+12)=0\\\\-x^2(x(x+4)+3(x+4))=0\\\\-x^2(x+4)(x+3)=0`

Hence the zeros of f(x) are 0,0,-4,-3.