Answer:
The values are evaluated below.
Explanation:
Given function is
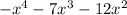
We have to find the domain, range, rel max, rel min, end behaviour, increasing or decreasing intervals and zeros of polynomial.
Domain:
The domain of a function is the set of all possible values of x for the given function.
Here domain is set of all real numbers R.
Range:
The range is the resulting y-values we get after substituting all the possible x-values.From the graph we see that
The range is

Relative maxima and minima of a function, are the largest and smallest value of the function on an entire domain of function.
Relative max of
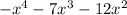 is 0 at x=0
is 0 at x=0
and
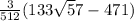 at
at
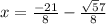
Relative min is
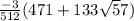 at
at
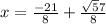
From the graph we see that
End behaviour is As

Increasing intervals and decreasing intervals are
Increasing:

Decreasing:
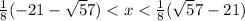
Zeroes are :
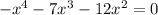
⇒
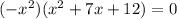
⇒
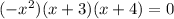
Hence, zeroes are 0, 0, -3, -4