Question

Kevin cycles 18 miles every morning as part of his exercise. The time it takes him to complete the distance varies inversely as the speed at which he rides. Which equation best models the amount of time it takes him to finish with his cycling, t, if he rides at a speed of m miles per hour?

A. T=18/m

B. T=18m

C. T=18+m

D. T=m/18

Answer 1

The
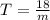`T = (18)/(m)` best models the amount of time it takes him to finish with kelvin cycling .

Option (A) is correct.

Explanation:

As given

Kevin cycles 18 miles every morning as part of his exercise.

The time it takes him to complete the distance varies inversely as the speed at which he rides.

`Time \propto (1)/(Speed)`

`Time = (Distance)/(Speed)`

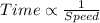
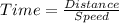
As m miles per hour is represented the speed.

T is the time taken by Kevin cycle for morning exercise .

Distance = 18

Putting the values in the above

`T = (18)/(m)`

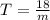
Therefore the
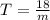`T = (18)/(m)` best models the amount of time it takes him to finish with kelvin cycling .

Option (A) is correct.