Question

AREA, PERMITER AND VOLUME QUESTIONS.

Hi guys,
Whoever can help me with the following questions will be my lifesaver.
QUESTION 1:
You have also been asked to help set up the basketball court.

(SEE DIAGRAM)
What is the circumference of the circle in m?

(C = πd)

What is the area of the circle?

(A = πr2)
----------------------------------------------
QUESTION 2:

The rectangular backboard of a basketball court needs to be assembled. Its area is given as 18,900 cm2 and the width as 1.8 m.
What is the backboard’s length in metres?
The seating space around the basketball court is shown below:
( SEE DIAGRAM)
What is the perimeter of the total area in m?
What is the area of the seating space in m2?
-------------------------------------------
QUESTION 3:

The arena will also have a children’s assault course in one area. As part of this, a climbing structure needs to be built in the shape of a pyramid. Look at the diagram below.

Formula for area of a triangle: A = b x h/ 2

(SEE DIAGRAM)

What is the area of this shape? m2?
--------------------------------------------------

QUESTION 4:
The area of the indoor sports exhibition is shown below. Use the following formulae:

Perimeter of a rectangle = 2l + 2w

Circumference of a circle = πd, π= 3.14

Area of a rectangle = lw

Area of a circle = πr2

( SEE DIAGRAM)

What is its perimeter in m?

What is its area m2?

Answer 1

1.

Part 1: Circumference is 11.31 meters

Part 2: Area is 10.18 square meters

2.

Part 1: Backboard's Length = 1.05 meters

Part 2: Perimeter is 187.8 meters

Part 3: Area of seating space is 178 square meters

3. Area is 21 square meters.

4.

Part 1: Perimeter is 255.41 meters

Part 2: Area is 3097.97 square meters.

Explanation:

Question 1:

Part 1:

The formula for the circumference of a circle is given by:

`C=\pi d\\C=\pi (2r)\\C=2\pi r`

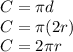
Where radius (r) is half of diameter (d)

Since radius of the circle shown in 1.8m, we plug it in the formula and get:

`C=2\pi r\\C=2\pi (1.8)\\C=11.31`

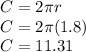
So C = 11.31 meters

Part 2:

The area of the circle is given by the formula:

`A=\pi r^2`

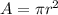
Where A is the area and r is the radius

Since we know r = 1.8, we plug it in the formula and find area:

`A=\pi r^2\\A=\pi(1.8)^2\\A=10.18`

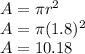
Area is 10.18 sq. meters.

Question 2:

Part 1:

Area of a rectangle is length * width

width is given in 1.8 m, which in cm, is 1.8 multiplied by 100, so we have

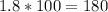`1.8*100=180`cm

To find Length, we plug area equal to 18,900 and width equal to 180 cm and solve:

`A=length*width\\18,900=length*180\\length=(18,900)/(180)\\length=105`

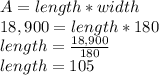
Length is 105 cm, in meters, we divide by 100, to get
`(105)/(100)=1.05`

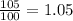
Backboard's Length = 1.05 meters

Part 2:

Perimeter means the sum of all the sides of the figure (however many sides it might have). If you look at the seating space, it has 8 sides, 4 of the outer sides and 4 of the inner sides. We just add all of them to get the perimeter.

Perimeter =
`18.4+32.5+18.4+32.5+15+28+15+28=187.8`

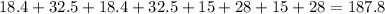
Thus the perimeter is 187.8 meters

Part 3:

Area of the seating space can be written as:

Area of seating space = area of big rectangle - area of basketball court

Area of big rectangle is length * width =
`18.4*32.5=598`

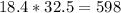
Area of basket ball court is length * width =
`15*28=420`

Now,

Area of seating space = 598 - 420 = 178 square meters.

Question 3:

Area shape consists of 4 same triangles (with base of 3 and height of 2) & 1 square (with side 3) in the middle.

To get the area of the shape we add area of 4 triangles & area of square.

Area of 1 triangle is

`A=(1)/(2)*b*h=(1)/(2)*3*2=3`

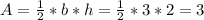
Area of 4 of the triangles is

`4*3=12`

Now, area of square is given by (side * side):

`A=s^2=3^2=9`

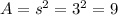
Area of square is 9

Hence, area of shape = 12+9=21 square meters

Question 4:

Part 1:

The perimeter is sum of all the sides of the figure. If we start from left side (4000cm) and go clockwise, we can identify all the sides.

• Starting side is 4000 cm side. 4000cm divided by 100 (to get it into meters): 40 m
• top is 10 m and 68 m = 78 m
• right side is 33 m
• then we have semicircle, since whole circle's circumference (perimeter) is
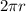  `2\pi r`, semicircle's perimeter is half of that so
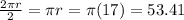  `(2\pi r)/(2)=\pi r=\pi (17)=53.41`m
• then a side of 34 m (bottom)
• then 700 cm , in meters we divide by 100, so 7m
• then 10 m is the last one before we come to starting point

Perimeter =
`40+10+68+33+53.41+34+7+10=255.41`

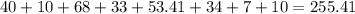
Perimeter is 255.41 meters

Part 2:

Area of the figure can be found by dividing the figures. From left, we can see that the whole figure consists of

• Left rectangle with length 40 m and width 10 m. Thus area of rectangle is length * width = 40 * 10 = 400
• Then another rectangle with length 68 m and width 33 m. Thus area of this rectangle is length * width = 68 * 33 = 2244
• Lastly in the bottom we have half a circle, area of whole circle is
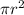  `\pi r^2` and that of this semicircle is half of this so area is
  `(\pi r^2)/(2)=(\pi (17)^2)/(2)=453.96`

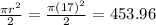
Adding all these we get the area of the figure:

Area =
`400+2244+453.96=3097.96`

Area is 3097.97 square meters.

Answer 2

Explanation:

(A) The radius of the circle is=1.8m

Then diameter will be: 2r=
`2{*}1.8=3.6 m`

Circumference of circle=
`{\pi}d`=
`3.14{*}3.6=11.304 m`

Area of the circle=
`{\pi}r^(2)=3.14{*}(1.8)^(2)=10.17 m^(2)`

(B) The area of the rectangular backboard of basketball court = 18900
`cm^(2)`

Width=180cm

Area of rectangle= l{\times}b[/tex]

18900=l{\times}180[/tex]

`l=105 cm=1.05m`

Perimeter of the seating space=2(l+b)

=
`2(32.5+18.4)`

=
`101.8 m`

Perimeter of the basketball court=2(l+b)

=
`2(15+28)`

=
`86 m`

Now, total perimeter= perimeter of the basketball court+perimeter of the seating space.

Total perimeter=
`101.8+86=187.8 m`

Area of the seating space=
`l{*}b`

=
`32.5{*}18.4=598 m^(2)`

(C) The shape consists of one square and 4 triangles, therefore area of square=
`(side)^(2)=(3)^(2)=9 m^(2)`

Area of 4 triangles=
`4{*}((1)/(2){*}B{*}H)`

=
`4{*}((1)/(2){*}3{*}2)=12m^(2)`

Area of the shape= Area of the square+ area of the 4 triangles

=
`9+12=21m^(2)`

(D) Perimeter of rectangle with length=40 m (After converting cm to m) and breadth= 10 m is given by:
`2(l+b)=2(40+10)=100 m`

Perimeter of rectangle with length 68 m and breadth=33 m is given by:
`2(l+b)=2(68+33)=202 m`

Perimeter of the semicircle=
`\frac{{\pi}d}{2}=\frac{3.14{*}34}{2}=53.38 m`

Total perimeter=
`100+201+53.38=355.38 m`

Area of rectangle with length=40 m (After converting cm to m) and breadth= 10 m is given by:
`l{*}b=40{*}10=400 m^(2)`

Area of rectangle with length 68 m and breadth=33 m is given by:
`l{*}b=68{*}33=2244 m^(2)`

Area of the semi circle=
`\frac{{\pi}r^(2)}{2}=\frac{3.14{*}17^(2)}{2}=453.73 m^(2)`

Total area=
`400+2244+453.73=3097.73 m^(2)`