Question

What is the quotient of the rational expression shown below? Make sure your answer is in reduced form x^2-4/x+3 divided x^2-4x+4/4x+2

Answer 1

I think the answer is 4(x+2)/x-2

Answer 2

see explanation

Explanation:

Given

`(x^2-4)/(x+3)` ÷
`(x^2-4x+4)/(4x+2)`

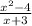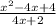
The first step is to factor numerators/denominators, if possible

x² - 4 = (x - 2)(x + 2) ← difference of squares

x² - 4x + 4 = (x - 2)(x - 2) ← perfect square

4x + 2 = 2(2x + 1)

To divide the expressions follow the steps

• Leave the first fraction

• Change division to multiplication

• Turn the second fraction upside down

We now have

`((x-2)(x+2))/(x+3)` ×
`(2(2x+1))/((x-2)(x-2))`

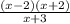Final step is to cancel common factors from the numerators/denominators

=
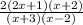`(2(2x+1)(x+2))/((x+3)(x-2))` ← quotient