Answer:
The coordinates of Y are (2,-0.2)
Explanation:
Let the coordinates of Y be (x,y)
Since M is the midpoint of XY, so
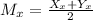
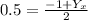
Multiply both sides by 2
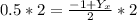
Cancel out the 2's from the top and bottom on the right side
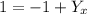
Add 1 to both sides
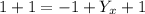
Cancel out -1 and +1 on the right side
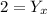
Flip the sides
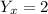
Similarly,
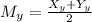

Multiply both sides by 2
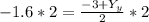
Cancel out the 2's on the top and bottom of the right side
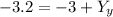
Add 3 to both sides
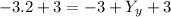
Cancel out -3 and +3 on the right side
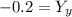
Flip the sides
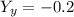
So, the coordinates of Y are (2,-0.2)