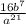Steps
So here are a few rules with exponents that we will be applying for this problem:
- Powering a power:

- Multiplying powers with the same base:
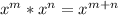
- Converting negative exponents to positive exponents:

Firstly, solve the outermost power:
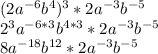
Next, multiply:
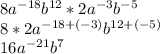
Finally, convert the negative exponents:
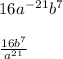
Answer
In short, your final answer is