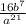Question

I need help on doing (2a^-6 b^4)^3 • 2a^-3 b^-5?

Answer 1

Steps

So here are a few rules with exponents that we will be applying for this problem:

• Powering a power:
  `(x^m)^n=x^(m*n)`
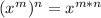
• Multiplying powers with the same base:
  `x^m*x^n=x^(m+n)`
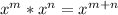
• Converting negative exponents to positive exponents:
  `x^(-m)=(1)/(m^n)\ \textsf{//}\ (1)/(x^(-m))=x^m`

Firstly, solve the outermost power:

`(2a^(-6) b^4)^3*2a^(-3) b^(-5)\\2^3a^(-6*3) b^(4*3)*2a^(-3) b^(-5)\\8a^(-18)b^(12)*2a^(-3)b^(-5)`

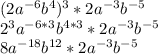
Next, multiply:

`8a^(-18)b^(12)*2a^(-3)b^(-5)\\8*2a^(-18+(-3))b^(12+(-5))\\16a^(-21)b^7`

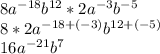
Finally, convert the negative exponents:

`16a^(-21)b^7\\\\(16b^7)/(a^(21))`

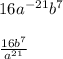
Answer

In short, your final answer is
`(16b^7)/(a^(21))`