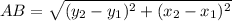Answer:
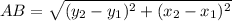
Explanation:
Given two points in grid which are not on the same horizontal line or vertical line. Hence, it will be like as shown in figure.
Let
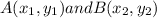 are the points on grid.
are the points on grid.
AO=(y-coordinate of A)-(y-coordinate o B)
=

OB=(x-coordinate of A)-(x-coordinate o B)
=

Hence, By Pythagoras theorem, distance between the points A and B i. AB can be calculated as
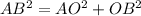
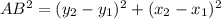
⇒