I need help with my algebra 2. I also want to know how to solve this.

Question

asked Sep 11, 2020 227k views

1 Answer

Frunkad · Answer 1 · 2020-09-16T01:24:26+0000

Add 1 to both sides:

√(x+3) = x+1

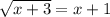
In cases like this, we have to remember that a root is always positive, so we can square both sides only assuming that

$x+1 \geq 0 \iff x \geq -1$

Under this assumption, we square both sides and we have

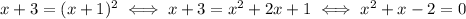
$x+3 = (x+1)^2 \iff x+3 = x^2+2x+1 \iff x^2+x-2 = 0$

The solutions to this equation are

$x = -2,\ x=1$

But since we can only accept solutions greater than -1, we discard
x=-2 and accept
x=1 .

In fact, we have

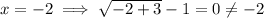
$x=-2 \implies √(-2+3)-1=0\\eq -2$

and

$x=1 \implies √(4)-1=1$

which is the only solution.