Answer:
The density (in g/mL) of water is 0.09888 g/mL.
The percentage error is 1.04%.
Step-by-step explanation:
The mass of an Erlenmeyer flask = m = 85.135 g
The mass of an Erlenmeyer flask and 100 mL of water ,M= 95.023 g
Mass of 10 mL water ,x= M - m = 95.023 g - 85.135 g = 9.888 g[/tex]
Mass of the wate ,x = 9.888 g
Volume of the water = V = 10 mL
Density of the water,d =
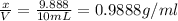 (calculated value)
(calculated value)
The density (in g/mL) of water is 0.9888 g/mL.
True density of the water , D'= 0.9992 g/mL(theoretical value)
The percent error can be calculated as:
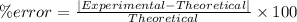
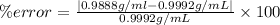
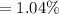
The percentage error is 1.04%.