Question

The product of the first three terms of a geometric progression is 3375, and their sum is 65. Find the first term of this progression.

Answer 1

15 hope this helps :)

Answer 2

5 or 45

Explanation:

For a geometric progression, the nth term is given by the formula Tn= arⁿ⁻¹, where a is the 1st term and r is the common ratio.

Alternatively, since r is the constant that we are multiplying to the previous term to obtain the next term, we can work out the 1st three terms as shown below:

1st term= a

2nd term= a ×r= ar

3rd term= ar ×r= ar²

Product of first 3 terms= 3375

a(ar)(ar²)= 3375

a³r³= 3375

(ar)³= 3375

Cube root both sides:

ar= 15

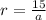`r = (15)/(a)` -----(1)

Given that the sum of the first 3 terms is 65,

a +ar +ar²= 65 -----(2)

Now that we have formed 2 equations, let's solve by substitution.

Substitute (1) into (2):

`a + a( (15)/(a) ) + a( \frac{15}{ {a} })^(2) = 65`

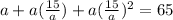
Expand:

`a + 15 + a( \frac{225}{ {a}^(2) } ) = 65`

`a + 15 + (225)/(a) = 65`

`a + (225)/(a) = 50`

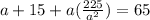
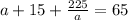
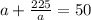
Multiply both sides by a:

a² +225= 50a

a² -50a +225= 0

Factorise:

(a -45)(a -5)= 0

a -45= 0 or a-5= 0

a= 45 or a= 5