Answer:
5 or 45
Explanation:
For a geometric progression, the nth term is given by the formula Tn= arⁿ⁻¹, where a is the 1st term and r is the common ratio.
Alternatively, since r is the constant that we are multiplying to the previous term to obtain the next term, we can work out the 1st three terms as shown below:
1st term= a
2nd term= a ×r= ar
3rd term= ar ×r= ar²
Product of first 3 terms= 3375
a(ar)(ar²)= 3375
a³r³= 3375
(ar)³= 3375
Cube root both sides:
ar= 15
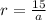 -----(1)
-----(1)
Given that the sum of the first 3 terms is 65,
a +ar +ar²= 65 -----(2)
Now that we have formed 2 equations, let's solve by substitution.
Substitute (1) into (2):
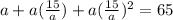
Expand:

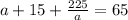
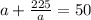
Multiply both sides by a:
a² +225= 50a
a² -50a +225= 0
Factorise:
(a -45)(a -5)= 0
a -45= 0 or a-5= 0
a= 45 or a= 5