The slope of the tangent line to the curve at (8, 2) is given by the derivative
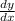 at that point. By the chain rule,
at that point. By the chain rule,
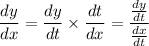
Differentiate the given parametric equations with respect to
 :
:

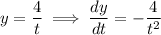
Then

We have
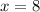 and
and
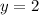 when
when
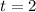 , so the slope at the given point is
, so the slope at the given point is
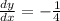 .
.
The normal line to the same point is perpendicular to the tangent line, so its slope is +4. Then using the point-slope formula for a line, the normal line has equation

Alternatively, we can eliminate the parameter and express
 explicitly in terms of
explicitly in terms of
 :
:
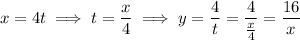
Then the slope of the tangent line is
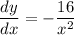
At
 , the slope is again
, the slope is again
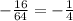 , so the normal has slope +4, and so on.
, so the normal has slope +4, and so on.