Question

Which of the following is a function equivalent to f(x) = 3(1.7)4x? (5 points) f(x) = 25.06x f(x) = 3(8.35)x f(x) = 3(8.25x) f(x) = 487.97x

Answer 1

Explanation:

Given: f(x) = 3(1.7)4x

This can also be looked at as: f(x) = 3 × 1.7 × 4 × x

You can multiply the three values four different ways and they will all be equivalent.

f(x) = (3 × 1.7) × 4 × x = 5.1(4)x

f(x) = 3 × (1.7 × 4) × x = 3(6.8)x

f(x) = 1.7 × (3 × 4) × x = 1.7(12)x

f(x) = 3 × 1.7 × 4 × x = 20.4x

Answer 2

`f(x)=3(8.35)^x`

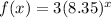
Explanation:

Here, the given exponential function,

`f(x) = 3(1.7)^(4x)`

`f(x)=3(1.7^4)^x` (
`a^(mn)=(a^m)^n` )

`f(x)=3(8.3521)^x`

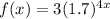
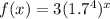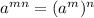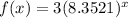
Since, two exponential functions are called equivalent when they can be written with same initial value and same growth or decay factor.

Now, 8.3521 can be written 8.35,

Thus, the function which is equivalent to the given function is,

`f(x)=3(8.35)^x`

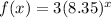
Note :

In exponential function
`ab^x`,

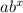a is the initial value,

And, b is the growth or decay factor.