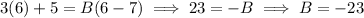Question

Find $A$ and $B$ such that

\[\frac{3x+5}{x^2-x-42}=\frac{A}{x-7}+\frac{B}{x+6}.\]Write your answer in the form $(A,B)$.

Answer 1

Assume

`(3x+5)/(x^2-x-42)=(3x+5)/((x-7)(x+6))=\frac A{x-7}+\frac B{x+6}`

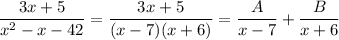
Combining the fractions on the right hand side gives

`(3x+5)/((x-7)(x-6))=(A(x-6)+B(x-7))/((x-7)(x-6))`

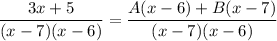
The fractions will be equal as long as the their numerator are equal:

`3x+5=A(x-6)+B(x-7)`

`3x+5=(A+B)x+(-6A-7B)`

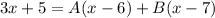
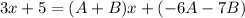
Polynomials are equal to one another if the coefficients of like terms are equal:

`\begin{cases}A+B=3\\-6A-7B=5\end{cases}`

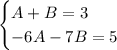
Solving this, you'd get
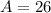`A=26` and
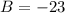`B=-23`, so that your answer would be (26, -23).

- - -

Instead of solving the system of equations above, there is a trick that involves picking
`x` so that some terms disappear and solving for either
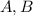`A,B` is much faster.

At the point where we have

`3x+5=A(x-6)+B(x-7)`

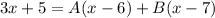
notice that setting
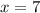`x=7` will eliminate
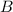`B`. Doing so, we get

`3(7)+5=A(7-6)\implies26=A`

while setting
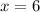`x=6` would give

`3(6)+5=B(6-7)\implies23=-B\implies B=-23`

Answer 2

We factor the denominator in the left-hand side to get

`\[(3x+5)/((x-7)(x+6))= (A)/(x - 7) + (B)/(x + 6).\]`

We then multiply both sides by

`$(x - 7)(x + 6)$`, to get
`\[3x + 5 = A(x + 6) + B(x - 7).\]`

We can solve for
`$A$` and
`$B$` by substituting suitable values of
`$x$`.

For example, setting
`$x = 7$`, the equation becomes
`$26 = 13A$`,

so
`$A = 2$`.

Setting
`$x = -6$`, the equation becomes
`$-13 = -13B$`,

so
`$B = 1$`

Therefore,
`$(A,B) = \boxed{(2,1)}$`.