Answer:
Minimum : -37 at x=2.4 and
Maximum = 37 at x=-2.4.
Step-by-step explanation:
Given:
 ; [-3,3]
; [-3,3]
Step-by-step explanation:
In order to find minimum/maximum of a function, we need to find the first derivative of the function and then set it equal to 0 to get critical points.
Therefore,
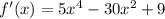
Setting derivative equal to 0, we get
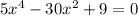
On applying quadratic formula, we get
x=2.4, -2.4, -0.7, 0.7.
So, those are critical points of the given function.
Plugging the values x=2.4, -2.4, -0.7, 0.7, -3 and 3 in above function, we get
f(2.4)=(2.4)^5-10(2.4)^3+9(2.4)= -37.01376 : Minimum.
f(-2.4)=(-2.4)^5-10(-2.4)^3+9(-2.4)= 37.01376 : Maximum.
f(0.7)=(0.7)^5-10(0.7)^3+9(0.7) = 3.03807
f(-0.7)=(-0.7)^5-10(-0.7)^3+9(-0.7) = -3.03807
f(-3)=(-3)^5-10(-3)^3+9(-3) =0
f(3)=(3)^5-10(3)^3+9(3) =0
Therefore the approximate values of the minimum and maximum points of f(x) =
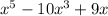 on [-3,3] are:
on [-3,3] are:
Minimum : -37 at x=2.4 and
Maximum = 37 at x=-2.4.