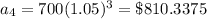Question

At the beginning of the year one Sam invests $700 at an annual compound interest rate of 5% he makes no deposit to or withdrawals from the account which explicit formula can be used to find account balance at the beginning of year 4 what is the balance

Answer 1

`a_n=700(1.05)^(n-1)`

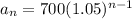
The balance would be $ 810.3375

Explanation:

Given,

The principal amount = $ 700,

Which is increasing with the compound rate of 5 %,

That is, every year the amount would be 105 % or 1.05 times of the previous amount,

Thus, we obtained a GP that can represents the given situation having first term, a = 700,

Common ratio, r = 1.05,

Since, the explicit formula of a GP is,

`a_n=ar^(n-1)`

`\implies a_n=700(1.05)^(n-1)`

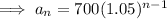
For the beginning of 4 year, n = 3,

Thus, the balance at the beginning of 4 years would be,

`a_(4)=700(1.05)^3=\$810.3375`