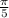Answer:
period of the function is
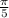
Explanation:
The given function is f (x) = cos 10x
Since cosine function is represented by
f (x) = a cos b x
where a = amplitude of cosine function and period =
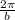
Now we compare function given with the standard form of cosine function.
we find b = 10
then period =
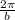
=
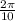
=
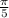
Therefore, period of the function is